Πίνακες και Λειτουργίες Δομών Δεδομένων

Όπως αναφέρεται στο σχολικό βιβλίο: Δομή Δεδομένων  είναι ένα σύνολο αποθηκευμένων δεδομένων που υφίσταται επεξεργασία από ένα σύνολο λειτουργιών. Ας μελετήσουμε κάθε μια λειτουργία και πως αυτή πραγματοποιείται σε έναν πίνακα (στατική δομή δεδομένων) με τη βοήθεια παραδειγμάτων :

Προσπέλαση: Πρόσβαση σε έναν κόμβο (κελί του πίνακα) με σκοπό να εξετασθεί ή τροποποιηθεί το περιεχόμενό του. Αυτό που συχνά ονομάζουμε και "σάρωμα" του πίνακα. Σχεδόν σε όλες τις ασκήσεις της ενότητας των ασκήσεων πραγματοποιείται προσπέλαση των πινάκων της εκάστοτε άσκησης με τη χρήση δομών επανάληψης, συνήθως με την δομή Για...από...μέχρι

Αλγόριθμος Προσπέλαση
   Δεδομένα // Ν, ΠΙΝΑΚΑΣ //
   Για i από 1 μέχρι Ν
         Εκτύπωσε "Το ", i, " στοιχείο του πίνακα είναι ", ΠΙΝΑΚΑΣ[i]
   Τέλος_επανάληψης
Τέλος Προσπέλαση

Εισαγωγή: Προσθήκη νέων κόμβων σε μια υπάρχουσα δομή δεδομένων. Ο πίνακας είναι στατική δομή δεδομένων και δεν υφίσταται η έννοια εισαγωγής νέου κόμβου. Όπως αναφέρεται και στην παράγραφο 3.3 του σχολικού βιβλίου το ακριβές μέγεθος της απαιτούμενης κύριας μνήμης καθορίζεται κατά τη στιγμή του προγραμματισμού.  Πραγματοποιείται προσθήκη νέου στοιχείου αλλά ουσιαστικά αυτό γίνεται με τη χρήση νέου πίνακα που έχει μια θέση περισσότερη από τον αρχικό πίνακα. Το νέο στοιχείο μπορεί να εισέλθει σε οποιαδήποτε θέση σύμφωνα με κάποιο κριτήριο π.χ. στο τέλος του πίνακα

Αλγόριθμος Προσθήκη
   Δεδομένα // Ν, ΠΙΝΑΚΑΣ //
   Διάβασε νέο_στοιχείο
   Για i από 1 μέχρι Ν   !  Τα στοιχεία 1 μέχρι Ν θα αντιγραφούν ως έχουν
         ΝΕΟΣ_ΠΙΝΑΚΑΣ[i] ← ΠΙΝΑΚΑΣ[i]
   Τέλος_επανάληψης
   ΝΕΟΣ_ΠΙΝΑΚΑΣ[Ν + 1] ← νέο_στοιχείο   !   Τοποθετείται το νέο στοιχείο
   Ν ← Ν + 1
   Αποτελέσματα // Ν, ΝΕΟΣ_ΠΙΝΑΚΑΣ //
Τέλος Προσθήκη

Διαγραφή: το αντίστροφο της εισαγωγής, δηλαδή αφαίρεση ενός κόμβου από μια δομή. Όπως αναφέρθηκε και στην εισαγωγή προηγουμένως δεν υφίσταται η έννοια της διαγραφής σε μια στατική δομή δεδομένων. Ουσιαστικά, μπορεί να δημιουργηθεί νέος πίνακας με ένα στοιχείο λιγότερο (σε μονοδιάστατο πίνακα) ή μια γραμμή/στήλη σε δισδιάστατο πίνακα, όπως πραγματοποιείται στην άσκηση 3.2.2.Ασκ2. Ας δούμε στη συνέχεια αλγόριθμο που διαγράφει το μεσαίο στοιχείο ενός πίνακα

Αλγόριθμος Διαγραφή_Μεσαιου_Στοιχείου
   Δεδομένα // Ν, ΠΙΝΑΚΑΣ //
   μεσαίο ← Ν div 2
   στοιχείο ← 0
   Για i από 1 μέχρι Ν     !   Τα στοιχεία 1 μέχρι Ν εκτός του στοιχείου Ν/2 θα αντιγραφούν ως έχουν 
       Αν (i <> μεσαίο) τότε
             στοιχείο ← στοιχείo + 1
             ΝΕΟΣ_ΠΙΝΑΚΑΣ[στοιχείο] ← ΠΙΝΑΚΑΣ[i]
       Τέλος_αν
   Τέλος_επανάληψης
   Ν ← στοιχείο      !   στοιχείο = Ν - 1
   Αποτελέσματα // Ν, ΝΕΟΣ_ΠΙΝΑΚΑΣ //
Τέλος Διαγραφή_Μεσαιου_Στοιχείου

Αναζήτηση: Προσπελαύνονται οι κόμβοι της δομής δεδομένων, προκειμένου να εντοπιστούν ένας ή περισσότεροι που έχουν μια συγκεκριμένη ιδιότητα.

- Αλγόριθμος σειριακής αναζήτησης (παράγραφος 3.6 σχολ. βιβλίου)

Ο αλγόριθμος σειριακής αναζήτησης, όπως παρουσιάζεται στο βιβλίο έχει ως εξής:

Αλγόριθμος Sequential_Search
   Δεδομένα // n, table, key //
   done ← ψευδής
   position ← 0
   i ← 1
   Όσο (done = ψευδής) και (i <= n) επανάλαβε
       Αν (table[i] = key) τότε
           done ← αληθής
           position ← i    
       Αλλιώς
           i ← i + 1
       Τέλος_αν
   Τέλος_επανάληψης
   Αν (done = αληθής) τότε
       Εκτύπωσε "Το στοιχείο ", key, " ευρέθη στη θέση ", position
   Αλλιώς
       Εκτύπωσε "Το στοιχείο ", key, " δεν ευρέθη στον δοθέντα πίνακα"      
   Τέλος_αν
   Αποτελέσματα // done, position //
Τέλος Sequential_Search




Ή εναλλακτικά χρησιμοποιώντας τη δομή Μέχρις_Ότου

   Αρχή_επανάληψης
       Αν (table[i] = key) τότε
           done ← αληθής
           position ← i    
       Αλλιώς
           i ← i + 1
       Τέλος_αν
   Μέχρις_ότου (done = αληθής) ή (i > n)

Παρατηρήσεις:

1.    Η αναζήτηση σταματά μόλις εντοπίσει κάποιο στοιχείο που είναι ίσο με την αναζητούμενη τιμή. Ο αλγόριθμος Παραλλαγή Νο 1 στη συνέχεια αποτελεί τροποποίηση του αλγορίθμου σειριακής αναζήτησης ώστε να καλύπτει την αδυναμία αυτή και συνεχίζει την αναζήτηση ώστε να εντοπίσει όλες τις τιμές του πίνακα table που έχουν τιμή ίση με τη μεταβλητή key.

2.    Ο πίνακας table δεν είναι ταξινομημένος. Ο αλγόριθμος Παραλλαγή Νο 2 στη συνέχεια αποτελεί τροποποίηση του αλγορίθμου σειριακής αναζήτησης ώστε να καλύπτει την αδυναμία αυτή και σταματά την αναζήτηση μόλις συναντήσει κάποιο στοιχείο του πίνακα table που είναι μεγαλύτερο από το ζητούμενο (μεταβλητή key) σε ταξινομημένο πίνακα.

Παραλλαγή Νο 1: Τροποποίηση του αλγορίθμου σειριακής αναζήτησης ώστε να αναζητά όλες τις θέσεις που βρίσκεται η αναζητούμενη τιμή

Για την αποφυγή τερματισμού του βρόχου αναζήτησης, εξαλείφουμε την μεταβλητή done από ολόκληρο το πρόγραμμα. Είναι προφανές ότι η τιμή που αναζητούμε στον πίνακα (μεταβλητή key) μπορεί να βρίσκεται σε περισσότερες από μια θέσεις του πίνακα table. Αν δεν επιθυμούμε περαιτέρω επεξεργασία των θέσεων αυτών απλά τις εκτυπώνουμε

Ωστόσο, υπάρχει η περίπτωση οι θέσεις αυτές να πρέπει να αποθηκευθούν ώστε να χρησιμοποιηθούν σε κάποιο άλλο σημείο του αλγορίθμου. Πώς πρέπει να αποθηκεύσουμε τις θέσεις αυτές; Δεδομένου ότι δεν γνωρίζουμε εξ αρχής το πλήθος των δεδομένων δεν μπορούμε να χρησιμοποιήσουμε μεταβλητές για το σκοπό αυτό. Κατά συνέπεια, πρέπει να χρησιμοποιήσουμε έναν άλλο πίνακα (έστω με όνομα POSITION_TABLE) ώστε να καταχωρούνται σε αυτόν οι θέσεις του πίνακα table που εντοπίστηκε η τιμή της μεταβλητής key

Το μέγεθος του πίνακα POSITION_TABLE είναι n καθώς πρέπει να καλύψουμε την ακραία περίπτωση να υπάρχουν και στις n θέσεις του πίνακα table η τιμή που έχει η μεταβλητή key. Η μεταβλητή count_found θα περιέχει το πλήθος των θέσεων που ικανοποιούν την αναζήτηση. Ο αλγόριθμος παρουσιάζεται εναλλακτικά με δυο τρόπους. Αφού επιθυμούμε να σαρώσουμε ολόκληρο τον πίνακα αυτό μπορεί να γίνει με την δομή επανάληψης Για…από…μέχρι αντί για την Όσο…επανάλαβε που χρησιμοποιήθηκε στα προηγούμενα παραδείγματα.

                                                           Αλγόριθμος Sequential_Search_Non_Stop
                                                               Δεδομένα // n, table, key //
                                                               count_found ←0

i ← 1
Όσο (i <= n) επανάλαβε
    Αν (table[i] = key) τότε
        count_found ← count_found + 1
        POSITION_TABLE[count_found] ← i
        Εκτύπωσε "Το στοιχείο ", key, " ευρέθη στη θέση", i        
    Τέλος_αν
    i ← i + 1
Τέλος_επανάληψης

Για i από 1 μέχρι n
   Αν (table[i] = key) τότε
       count_found ← count_found + 1
       POSITION_TABLE[count_found] ← i
       Εκτύπωσε "Το στοιχείο ", key, " ευρέθη στη θέση", i
   Τέλος_αν
Τέλος_επανάληψης

                                                        Αν (count_found <> 0) τότε
                                                            Εκτύπωσε "Το στοιχείο ", key, " εντοπίστηκε σε ", count_found, " θέσεις"
                                                        Αλλιώς
                                                            Εκτύπωσε "Δεν βρέθηκε κανένα στοιχείο"
                                                        Τέλος_Αν
                                                        Αποτελέσματα // count_found, POSITION_TABLE //
                                                    Τέλος Sequential_Search_Non_Stop


Παραλλαγή Νο 2: Τροποποίηση του αλγορίθμου σειριακής αναζήτησης ώστε να λειτουργεί βέλτιστα σε ταξινομημένο πίνακα

Αλγόριθμος Sequential_Search_Sorted_Table
  Δεδομένα // n, table, key //
   done ← ψευδής
   position ← 0
   i ← 1
   Όσο (done = ψευδής) και (i <= n) επανάλαβε  ! για ταξινομημένο πίνακα με αύξουσα διάταξη
      Αν (table[i] > key) τότε  ! σταμάτα την επανάληψη, δεν θα βρεθεί το στοιχείο
          done ← αληθής
      Αλλιώς_Αν (table[i] = key) τότε   ! σταμάτα την επανάληψη, το στοιχείο βρέθηκε
          done ← αληθής
          position ← i
      Αλλιώς  ! συνέχισε την την επανάληψη
          i ← i + 1
      Τέλος_αν
   Τέλος_επανάληψης
   Αν (position <> 0) τότε
      Εκτύπωσε "Το στοιχείο ", key, " ευρέθη στη θέση ", position
   Αλλιώς
      Εκτύπωσε "Το στοιχείο ", key, " δεν ευρέθη στον δοθέντα πίνακα"
   Τέλος_αν
   Αποτελέσματα // position //
Τέλος Sequential_Search_Sorted_Table

Παρατηρήσεις:

Η αναζήτηση σταματά όταν η τιμή προς αναζήτηση (μεταβλητή key) είναι μικρότερη από την τρέχουσα τιμή του πίνακα table

Σε αυτήν την περίπτωση δεν έχει νόημα να συνεχιστεί η αναζήτηση καθώς δεν αναμένεται να έχει επιτυχές αποτέλεσμα

 4   9   12   19   23   45   53   67 

Για παράδειγμα η αναζήτηση για την τιμή 14 στον παραπάνω πίνακα δεν έχει νόημα να συνεχιστεί μετά την 4η επανάληψη (i=4, table[i]=19) καθώς ο αριθμός 14 που είναι μικρότερος του 19 αποκλείεται να βρίσκεται σε κάποια από τις επόμενες θέσεις του πίνακα. Έτσι, αποφεύγονται άσκοπες επαναλήψεις. Το αν εντοπίστηκε ή όχι η τιμή key το ανιχνεύουμε με τη μεταβλητή position και όχι με την done καθώς η τελευταία λαμβάνει την τιμή αληθής ακόμη κι αν δεν ευρέθη η key

Ταξινόμηση: Οι κόμβοι μιας δομής διατάσσονται κατά αύξουσα ή φθίνουσα διάταξη.

- Αλγόριθμος ταξινόμησης ευθείας ανταλλαγής – φυσαλίδας (παράγραφος 3.7 του σχολ. βιβλίου)

Ο αλγόριθμος ταξινόμησης ευθείας ανταλλαγής όπως παρουσιάζεται στο βιβλίο έχει ως εξής:

Αλγόριθμος Φυσσαλίδα
  Δεδομένα // n, table //
  Για i από 2 μέχρι n
    Για j από n μέχρι i με_βήμα –1
        Αν table[j - 1] > table[j] τότε    ! αύξουσα ταξινόμηση
            temp ← table[j - 1]
            table[j - 1] ← table[j]
            table[j] ← temp
        Τέλος_αν
    Τέλος_επανάληψης
  Τέλος_επανάληψης
  Αποτελέσματα // table //
Τέλος Φυσσαλίδα

Παρατηρήσεις:

- Η εντολή αντιμετάθεσε ορίζεται στην ψευδογλώσσα και μπορούμε να τη χρησιμοποιήσουμε σε αλγορίθμους αλλά καλό να την αποφεύγουμε καθώς δεν ορίζεται στη ΓΛΩΣΣΑ και δεν μπορούμε να τη χρησιμοποιήσουμε σε προγράμματα

- Η διάταξη της ταξινόμησης είναι αύξουσα. Για φθίνουσα ταξινόμηση, αρκεί να αντιστραφεί η φορά της συνθήκης της δομής επιλογής Αν

- Ο πίνακας table είναι μονοδιάστατος (εφαρμογή σε δισδιάστατο πίνακα - με ταξινόμηση κάποιας στήλης παρουσιάζεται στην άσκηση)

Το σχολικό βιβλίο παραθέτει ένα παράδειγμα για την καλύτερη κατανόηση του αλγορίθμου

Παρατηρούμε στο επόμενο σχήμα  την «εικόνα» του πίνακα στο τέλος κάθε επανάληψης της εξωτερικής δομής Για

Από την τελευταία θέση του πίνακα έως την i, αν η τιμή κάποιου κελιού του πίνακα είναι μικρότερη από αυτή του επόμενου κελιού, τότε αντιμεταθέτουμε τις τιμές τους. Έτσι, αν υπάρχει κάποιος μικρός αριθμός σε "χαμηλή" θέση στον πίνακα διαδοχικά "ανεβαίνει" σε "υψηλότερες" θέσεις όπως μια φυσαλίδα στο υγρό

Ας δούμε όμως και ένα άλλο παράδειγμα, θέλουμε να ταξινομήσουμε τον πίνακα:     

 3 

 16 

 11 

 1 

 8 

Το εξωτερικό Για επιβάλλει την εκτέλεση 4 βημάτων. Αυτά είναι τα εξής:

i = 2
j = 5 j = 4 j = 3 j = 2
 3 
 16 
 11 
 1 
 8 
 3 
 16 
 1 
 11 
 8 
 3 
 1 
 16 
 11 
 8 
 1 
 3 
 16 
 11 
 8 
Αλλαγή:  Όχι Ναι Ναι Ναι

Παρατηρούμε, ότι ο μικρότερος αριθμός έχει βρεθεί στην πρώτη θέση του πίνακα. Στη συνέχεια:

i = 3
j = 5 j = 4 j = 3
 1 
 3 
 16 
 8 
 11 
 1 
 3 
 8 
 16 
 11 
 1 
 3 
 8 
 16 
 11 
Αλλαγή:  Ναι Ναι Όχι

Παρατηρούμε, ότι οι δυο πρώτες θέσεις περιέχουν τους δυο μικρότερους αριθμούς του πίνακα. Στη συνέχεια:

i = 4
j = 5 j = 4
 1 
 3 
 8 
 11 
 16 
 1 
 3 
 8 
 11 
 16 
Αλλαγή:  Ναι Όχι

Παρατηρούμε, ότι οι έχει ολοκληρωθεί η ταξινόμηση αλλά πρέπει να εκτελέσουμε ακόμη ένα βήμα που δεν θα προκαλέσει αλλαγές στον πίνακα

i = 5
j = 5
 1 
 3 
 8 
 11 
 16 
Αλλαγή:  Όχι

Με την κατάλληλη τροποποίηση του αλγορίθμου της φυσαλίδας όπως παρουσιάζεται στο βιβλίο μπορούμε να αποφύγουμε την εκτέλεση περιττών βημάτων. Αυτό μπορεί να  επιτευχθεί με τη βοήθεια μίας λογικής μεταβλητής, που σε κάθε νέα επανάληψη του εξωτερικού βρόχου αρχικοποιείται ως ψευδής και αλλάζει ως αληθής αν σε κάποιο πέρασμα γίνει έστω και μία ανταλλαγή. Έτσι, αν σε κάποιο πέρασμα δεν εκτελεσθεί καμία ανταλλαγή, τότε η σημαία παραμένει ψευδής και αυτομάτως τελειώνει ο αλγόριθμος

Αλγόριθμος Φυσσαλίδα_Τροποποίηση
  Δεδομένα // n, table //
  i ← 2
  Αρχή_επανάληψης
    έγινε_αντιμετάθ ← ψευδής
    Για j από n μέχρι i με_βήμα –1
        Αν table[j - 1] > table[j] τότε    ! αύξουσα ταξινόμηση
            temp ← table[j - 1]
            table[j - 1] ← table[j]
            table[j] ← temp
            έγινε_αντιμετάθ ← αληθής
        Τέλος_αν
    Τέλος_επανάληψης
    i ← i + 1
  Μέχρις_ότου (i > n) ή (έγινε_αντιμετάθ = ψευδής)
  Αποτελέσματα // table //
Τέλος Φυσσαλίδα_Τροποποίηση

Μια άλλη προσέγγιση παρουσιάζεται στην παράγραφο 3.3 δραστηριότητα ΔΤ2 τετράδιο μαθητή. Αυτή είναι:

Αλγόριθμος Φυσσαλίδα_Τροποποίηση2
  Δεδομένα // n, table //
  Αρχή_επανάληψης
    έγινε_αντιμετάθ ← ψευδής
    Για i από 1 μέχρι n
        Αν table[i + 1] < table[i] τότε    ! αύξουσα ταξινόμηση
            temp ← table[i + 1]
            table[i + 1] ← table[i]
            table[i] ← temp
            έγινε_αντιμετάθ ← αληθής
        Τέλος_Αν
    Τέλος_επανάληψης
  Μέχρις_ότου (έγινε_αντιμετάθ =  ψευδής)
  Αποτελέσματα // table //
Τέλος Φυσσαλίδα_Τροποποίηση2

- Αλγόριθμος ταξινόμησης με επιλογή (παράγραφος 4.2.1 τετραδίου μαθητή και βιβλίο καθηγητή)

Αλγόριθμος Tαξινόμηση_με_επιλογή
  Δεδομένα // n, table //
  Για i από 1 μέχρι n
      j ← i
      Για από i + 1 μέχρι n
          Αν table[k] < table[j] τότε
              j ← k
          Τέλος_αν
      Τέλος_επανάληψης
      temp ← table[j]
      table[j] ← table[i]
      table[i] ← temp
  Τέλος_επανάληψης
  Αποτελέσματα // table //
Τέλος Tαξινόμηση_με_επιλογή

Ο αλγόριθμος βασίζεται στην επιλογή του μικρότερου στοιχείου από αυτά που δεν έχουν ταξινομηθεί μέχρι τώρα

Για κάθε στοιχείο δηλαδή από το πρώτο μέχρι το τελευταίο, ελέγχεται ποιο από τα στοιχεία που ακολουθούν είναι μικρότερο και αν υπάρχει τέτοιο τα περιεχόμενα των δυο θέσεων αντιμετατίθενται. Η μέθοδος αυτή παρουσιάζεται στο επόμενο σχήμα καθώς εφαρμόζεται σε μονοδιάστατο πίνακα. Το ταξινομημένο τμήμα του πίνακα εμφανίζεται με σκίαση, ενώ με τα βέλη εμφανίζονται τα στοιχεία που ανταλλάσσονται αμοιβαία. Λόγου χάριν, στην πρώτη σειρά βρίσκουμε ότι το στοιχείο 5 είναι το μικρότερο και αντιμετατίθεται με το πρώτο στοιχείο του πίνακα, το 52. Έτσι προκύπτει η μορφή του πίνακα στη δεύτερη σειρά. Στη συνέχεια η διαδικασία προχωρεί με την ίδια λογική μέχρι την τελική ταξινόμηση του πίνακα


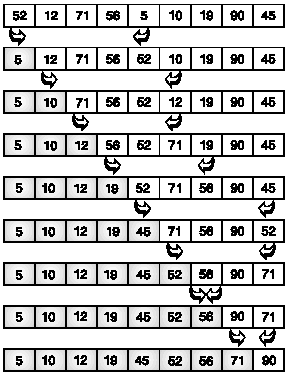
- Αλγόριθμος ταξινόμησης ευθείας εισαγωγής (δραστηριότητα ΔΣ3 τετράδιο μαθητή, κεφάλαιο 3)

Ο αλγόριθμος αυτός είναι ιδανικός για περιπτώσεις δεδομένων "περίπου" ταξινομημένων. Παρουσιάζεται στη συνέχεια

Αλγόριθμος Tαξινόμηση_με_ευθεία_εισαγωγή
  Δεδομένα // table, n //
  Για i από 2 μέχρι n
      temp ← table[i]
      j ← i - 1
      done ← ψευδής
      Όσο done = ψευδής επανάλαβε
          Αν j = 0 τότε    ! φτάσαμε στην αρχή του πίνακα, άρα πρέπει να σταματήσουμε
             done ← αληθής
          Αλλιώς_αν temp < table[j] τότε    ! βρήκαμε ένα μεγαλύτερο στοιχείο, άρα πρέπει να σταματήσουμε
             table[j + 1] ← table[j]
             j ← j - 1
          Αλλιώς    ! πρέπει να σταματήσουμε την επανάληψη γιατί το στοιχείο θα μείνει σε αυτήν τη θέση
             done ← αληθής
          Τέλος_αν
      Τέλος_επανάληψης
      table[j + 1] ← temp
  Τέλος_επανάληψης
  Αποτελέσματα // table //
Τέλος Tαξινόμηση_με_ευθεία_εισαγωγή

Η τεχνική είναι η εξής: συγκρίνουμε τον δεύτερο με τον πρώτο αριθμό και αν χρειαστεί τους αντιμεταθέτουμε ώστε ο πρώτος να είναι μεγαλύτερος. Στη συνέχεια ελέγχουμε τον τρίτο και τον τοποθετούμε στη χωστή θέση σε σχέση με τους 2 πρώτους (αν χρειαστεί μετακινούμε μια θέση τους αριθμούς που είναι μεγαλύτερη ώστε να τοποθετηθεί). Το ίδιο επαναλαμβάνουμε για όλους τους αριθμούς. Ακολουθεί παράδειγμα:

 

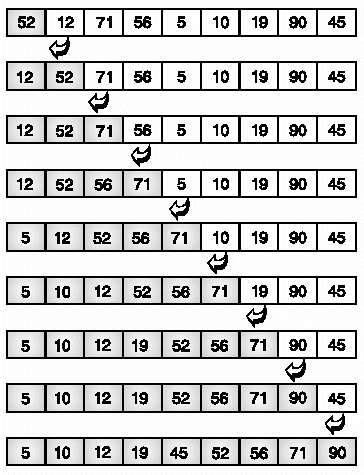
Αντιγραφή: Όλοι ή μερικοί κόμβοι μιας δομής αντιγράφονται σε μία άλλη. Ας δούμε ένα παράδειγμα με τον αλγόριθμο που ακολουθεί: π.χ. Με δεδομένο μονοδιάστατο πίνακα αριθμών να δημιουργηθεί νέος πίνακας που περιέχει μόνο τους θετικούς άρτιους

Αλγόριθμος Αντιγραφή_Πίνακα
   Δεδομένα // Ν, ΠΙΝΑΚΑΣ //
   πλήθος ← 0
   Για i από 1 μέχρι Ν
       Αν (ΠΙΝΑΚΑΣ[i] > 0) και (ΠΙΝΑΚΑΣ[i] mod 2 = 0) τότε
             πλήθος ← πλήθος + 1
             ΝΕΟΣ_ΠΙΝΑΚΑΣ[πλήθος] ← ΠΙΝΑΚΑΣ[i]
       Τέλος_Αν
   Τέλος_επανάληψης
   Αποτελέσματα // πλήθος, ΝΕΟΣ_ΠΙΝΑΚΑΣ //
Τέλος Αντιγραφή_Πίνακα

Συγχώνευση: Δύο ή περισσότερες δομές συνενώνονται σε μια ενιαία δομή. Ο αλγόριθμος παρουσιάζεται στην παράγραφο 3.9.2 στο βιβλίο καθηγητή. Ας δούμε ένα παράδειγμα για την δεύτερη άσκηση με τη χρήση 2 ταξινομημένων πινάκων με αριθμητικά στοιχεία. Αρχικά λοιπόν, η εικόνα των πινάκων είναι η εξής:

Πίνακας Α:        

 1 

 5 

 8 

 11 

 16 

    i = 1  (δείκτης του πίνακα)

Πίνακας Β:        

 -2 

 4 

 9 

    j = 1  (δείκτης του πίνακα)

Τελικός Πίνακας:        
                                           

    μ = 0   (δείκτης του πίνακα)

Αρχικά λοιπόν, θα συγκριθούν τα στοιχεία A[1] = 1 και Β[1] = -2, οπότε το μικρότερο στοιχείο (-2) θα τοποθετηθεί στον τελικό πίνακα στην πρώτη θέση και η μεταβλητή μ θα αυξηθεί κατά 1

Πίνακας Α:        

 1 

 5 

 8 

 11 

 16 

    i = 1

Πίνακας Β:        

 -2 

 4 

 9 

    j = 2

Τελικός Πίνακας Γ:        

 -2 

                            

   μ = 1

Στη συνέχεια, θα συγκριθούν τα στοιχεία A[1] = 1 και Β[2] = 4, οπότε το μικρότερο στοιχείο (1) θα τοποθετηθεί στον τελικό πίνακα στην πρώτη θέση και η μεταβλητή μ θα αυξηθεί κατά 1 (θα γίνει 2)

Πίνακας Α:        

 1 

 5 

 8 

 11 

 16 

    i = 2

Πίνακας Β:        

 -2 

 4 

 9 

    j = 2

Τελικός Πίνακας Γ:        

 -2 

 1 

                        

   μ = 2

Στη συνέχεια, θα συγκριθούν τα στοιχεία A[2] = 5 και Β[2] = 4, οπότε το μικρότερο στοιχείο (4) θα τοποθετηθεί στον τελικό πίνακα στην πρώτη θέση και η μεταβλητή μ θα αυξηθεί κατά 1 (θα γίνει 3)

Πίνακας Α:        

 1 

 5 

 8 

 11 

 16 

    i = 2

Πίνακας Β:        

 -2 

 4 

 9 

    j = 2

Τελικός Πίνακας Γ:        

 -2 

 1 

 4 

                    

   μ = 3

Όπως γίνεται εύκολα αντιληπτό με την παραπάνω διαδικασία κάποια στιγμή εξαντλείται ο μικρότερος πίνακας και θα υπάρχει η παρακάτω εικόνα. Σε αυτήν την περίπτωση πρέπει να αντιγραφεί ο αρχικός πίνακας ως έχει:

Πίνακας Α:        

 1 

 5 

 8 

 11 

 16 

    i = 4

Πίνακας Β:        

 -2 

 4 

 9 

    j = 4

Τελικός Πίνακας Γ:        

 -2 

 1 

 4 

  5   8   9         

   μ = 6

Η τελική εικόνα είναι η εξής:

Πίνακας Α:        

 1 

 5 

 8 

 11 

 16 

    i = 7

Πίνακας Β:        

 -2 

 4 

 9 

    j = 4

Τελικός Πίνακας Γ:        

 -2 

 1 

 4 

  5   8   9   11   16 

   μ = 8

Διαχωρισμός: αντίθετη διαδικασία από τη συγχώνευση. Χαρακτηριστικό παράδειγμα αποτελεί  η άσκηση 3.1.2.Ασκ5. Ας δούμε ένα ακόμη παράδειγμα με τον αλγόριθμο που ακολουθεί: π.χ. Με δεδομένο μονοδιάστατο πίνακα αριθμών να δημιουργηθούν δυο νέοι πίνακες που περιέχουν του θετικούς και τους αρνητικούς αριθμούς

Αλγόριθμος Διαχωρισμός_Πινάκων
   Δεδομένα // Ν, ΠΙΝΑΚΑΣ //
   Ν1 ← 0
   Ν2 ← 0
   Για i από 1 μέχρι Ν
       Αν (ΠΙΝΑΚΑΣ[i] > 0) τότε
             Ν1 ← Ν1 + 1
             ΠΙΝΑΚΑΣ1[Ν1] ← ΠΙΝΑΚΑΣ[i]
       Αλλιώς
             Ν2 ← Ν2 + 1
             ΠΙΝΑΚΑΣ2[Ν2] ← ΠΙΝΑΚΑΣ[i]
       Τέλος_αν
   Τέλος_επανάληψης
   Αποτελέσματα // Ν1, ΠΙΝΑΚΑΣ1, Ν2, ΠΙΝΑΚΑΣ2 //
Τέλος Διαχωρισμός_Πινάκων

Ωστόσο, οι τυπικές επεξεργασίες πινάκων που πραγματοποιούμε σε ένα πίνακα είναι: υπολογισμός αθροίσματος, εύρεση ελαχίστου/μεγίστου, ταξινόμηση στοιχείων, αναζήτηση στοιχείου σε πίνακα, συγχώνευση πινάκων 

Ημερομηνία τελευταίας τροποποίησης: 1/11/2004
Επικοινωνία: Τσιωτάκης Παναγιώτης