ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ΄ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ
ΤΡΙΤΗ 30 ΜΑΙΟΥ 2006 - ΑΕΠΠ
ΘΕΜΑ 1ο
Α. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις 1-5 και δίπλα τη λέξη Σωστό, αν είναι σωστή, ή τη λέξη Λάθος, αν είναι λανθασμένη.
1. Η σειριακή αναζήτηση χρησιμοποιείται αποκλειστικά στους ταξινομημένους πίνακες.
2. Η εντολή επανάληψης ΓΙΑ … ΑΠΟ … ΜΕΧΡΙ … ΜΕ_ΒΗΜΑ μπορεί να χρησιμοποιηθεί, όταν έχουμε άγνωστο αριθμό επαναλήψεων.
3. Για την εκτέλεση μιας εντολής συμβολικής γλώσσας απαιτείται η μετάφρασή της σε γλώσσα μηχανής.
4. Η λίστα των πραγματικών παραμέτρων καθορίζει τις παραμέτρους στην κλήση του υποπρογράμματος.
5. Σε μία δυναμική δομή δεδομένων τα δεδομένα αποθηκεύονται υποχρεωτικά σε συνεχόμενες θέσεις μνήμης. Μονάδες 10
| Λύση |
| 1. Λ 2. Λ
3. Σ
4. Σ
5. Λ |
Β. Να αναφέρετε τους κανόνες που πρέπει να ακολουθούν οι λίστες των παραμέτρων κατά την κλήση ενός υποπρογράμματος. Μονάδες 9
| Λύση |
- Το πλήθος των πραγματικών και των τυπικών παραμέτρων είναι το ίδιο
- Κάθε πραγματική αντιστοιχίζεται στην τυπική που βρίσκεται στην ίδια θέση
- Η πραγματική και η αντίστοιχη τυπική πρέπει να έχουν τον ίδιο τύπο [Σελίδα 220] |
Γ. Δίνεται το παρακάτω πρόγραμμα και υποπρογράμματα:
ΠΡΟΓΡΑΜΜΑ Κύριο
ΜΕΤΑΒΛΗΤΕΣ
ΑΚΕΡΑΙΕΣ : Α, Β, Γ
ΑΡΧΗ
ΔΙΑΒΑΣΕ Α, Β, Γ
ΚΑΛΕΣΕ Διαδ1(Α, Β, Γ)
ΓΡΑΨΕ Α, Β, Γ
ΤΕΛΟΣ_ΠΡΟΓΡΑΜΜΑΤΟΣ
ΔΙΑΔΙΚΑΣΙΑ Διαδ1(Β, Α, Γ)
ΜΕΤΑΒΛΗΤΕΣ
ΑΚΕΡΑΙΕΣ : Α, Β, Γ
ΑΡΧΗ
Α <- Α + 2
Β <- Β - 3
Γ <- Α + Β
ΓΡΑΨΕ Α, Β, Γ
ΤΕΛΟΣ_ΔΙΑΔΙΚΑΣΙΑΣ
Τι θα εμφανιστεί κατά την εκτέλεση του προγράμματος, αν ως τιμές εισόδου δοθούν οι αριθμοί 5, 7, 10; Μονάδες 12
| Λύση |
| |
Κύριο Πρόγραμμα |
Διαδικασία |
| |
Α |
Β |
Γ |
Α |
Β |
Γ |
Κύριο πρόγραμμα – αρχικοποίηση |
5 |
7 |
10 |
|
|
|
Κλήση διαδικασίας |
|
|
|
7 |
5 |
10 |
Εκτέλεση διαδικασίας |
|
|
|
9 |
2 |
11 |
Επιστροφή στο κύριο πρόγραμμα |
2 |
9 |
11 |
|
|
|
Θα εμφανιστούν οι τιμές 9 2 11 και 2 9 11 |
Δ. Να γράψετε στο τετράδιό σας τους αριθμούς της Στήλης Α και δίπλα το γράμμα της Στήλης Β που αντιστοιχεί σωστά. Στη Στήλη Β υπάρχει ένα επιπλέον στοιχείο.
Μονάδες 5
Στήλη Α |
Στήλη Β |
1.
“ΑΛΗΘΗΣ” |
α. λογικός τελεστής |
2.
ΚΑΙ |
β. μεταβλητή |
3.
α > 12 |
γ. αλφαριθμητική σταθερά |
4.
αριθμός_παιδιών |
δ. λογική σταθερά |
5.
≤ |
ε. συγκριτικός τελεστής |
| |
στ. συνθήκη |
| Λύση |
| 1 – γ, 2 – α, 3 – στ, 4 – β, 5 – ε |
Ε. Αν α = 5, β = 7 και γ = 10, να χαρακτηρίσετε στο τετράδιό σας τις παρακάτω προτάσεις χρησιμοποιώντας μία από τις λέξεις ΑΛΗΘΗΣ ή ΨΕΥ∆ΗΣ. Μονάδες 4
Πρόταση Α. (όχι (α + 2 ≥ β)) ή β + 3 = γ
Πρόταση Β. α + 2 * β < 20 και 2 * α = γ
| Λύση |
Πρόταση Α. (όχι (5 + 2 ≥ 7)) ή 7 + 3 = 10 ~ (όχι (7 ≥ 7)) ή 10 = 10 ~ όχι Αληθής ή Αληθής ~ Αληθής
Πρόταση Β. α + 2 * β < 20 και 2 * α = γ ~ 5 + 2 * 7 < 20 και 2 * 5 = 10 ~ 19 < 20 και 10 = 10 ~ Αληθής και Αληθής ~ Αληθής |
ΘΕΜΑ 2ο
1. Δίνεται ο παρακάτω αλγόριθμος σε μορφή διαγράμματος ροής:
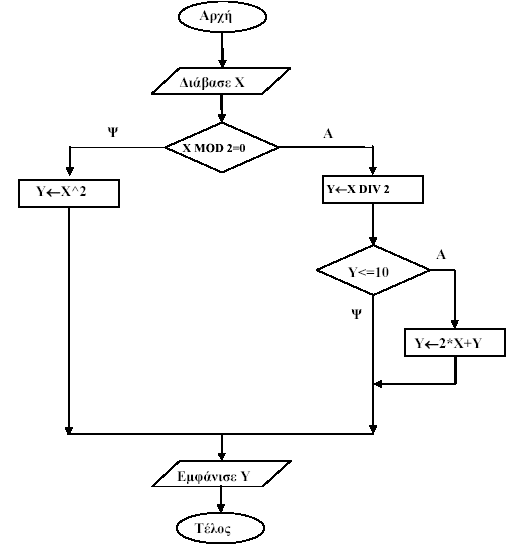
α. Να κατασκευάσετε ισοδύναμο αλγόριθμο σε ψευδογλώσσα. Μονάδες 7
β. Να εκτελέσετε τον αλγόριθμο για κάθε μία από τις παρακάτω τιμές της μεταβλητής Χ. Να γράψετε στο τετράδιό σας την τιμή της μεταβλητής Υ, όπως θα εμφανισθεί σε κάθε περίπτωση. Μονάδες 3
i. Χ = 9 ii. Χ = 10 iii. Χ = 40
| Λύση |
Αλγόριθμος Θέμα2α
Διάβασε Χ
Αν Χ mod 2 = 0 τότε
Υ ← Χ div 2
Αν Y <= 10 τότε
Υ ← 2 * Χ + Y
Τέλος_αν
Αλλιώς
Υ ← Χ ^ 2
Τέλος_αν
Εμφάνισε Υ
Τέλος Θέμα2α
Θα εμφανιστούν οι τιμές i. 81 ii. 25 iii. 20
|
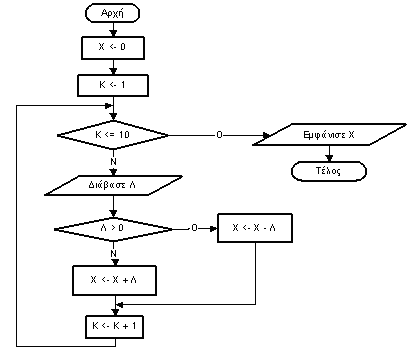
2. Δίνεται ο παρακάτω αλγόριθμος σε ψευδογλώσσα:
Αλγόριθμος Μετατροπή
Χ ← 0
Για Κ από 1 μέχρι 10
Διάβασε Λ
Αν Λ > 0 τότε
Χ ← Χ + Λ
Αλλιώς
Χ ← Χ - Λ
Τέλος_αν
Τέλος_επανάληψης
Εμφάνισε Χ
Τέλος Μετατροπή
Να σχεδιάσετε το αντίστοιχο διάγραμμα ροής. Μονάδες 10
ΘΕΜΑ 3ο
Σε ένα διαγωνισμό του ΑΣΕΠ εξετάζονται 1500 υποψήφιοι. Ως εξεταστικό κέντρο χρησιμοποιείται ένα κτίριο με αίθουσες διαφορετικής χωρητικότητας.
Ο αριθμός των επιτηρητών που απαιτούνται ανά αίθουσα καθορίζεται αποκλειστικά με βάση τη χωρητικότητα της αίθουσας ως εξής:
ΧΩΡΗΤΙΚΟΤΗΤΑ |
ΑΡΙΘΜΟΣ ΕΠΙΤΗΡΗΤΩΝ |
Μέχρι και 15 θέσεις |
1 |
Από 16 μέχρι και 23 θέσεις |
2 |
Πάνω από 23 θέσεις |
3 |
Να γίνει πρόγραμμα σε γλώσσα προγραμματισμού «ΓΛΩΣΣΑ» το οποίο:
α. για κάθε αίθουσα θα διαβάζει τη χωρητικότητά της, θα υπολογίζει και θα εμφανίζει τον αριθμό των επιτηρητών που χρειάζονται. Ο υπολογισμός του αριθμού των επιτηρητών να γίνεται από συνάρτηση που θα κατασκευάσετε για το σκοπό αυτό. Μονάδες 12
β. θα σταματάει όταν εξασφαλισθεί ο απαιτούμενος συνολικός αριθμός θέσεων. Μονάδες 8
Σημείωση: Να θεωρήσετε ότι η συνολική χωρητικότητα των αιθουσών του κτιρίου επαρκεί για τον αριθμό των υποψηφίων.
| Λύση |
ΠΡΟΓΡΑΜΜΑ ΑΣΕΠ
ΜΕΤΑΒΛΗΤΕΣ
ΑΚΕΡΑΙΕΣ : σύνολο, χωρητ, επιτηρητές
ΑΡΧΗ
σύνολο <– 0
ΟΣΟ (σύνολο < 1500) ΕΠΑΝΑΛΑΒΕ ! μπορούσε να χρησιμοποιηθεί και η Μέχρις_ότου
ΔΙΑΒΑΣΕ χωρητ
επιτηρητές <– Πόσοι_επιτ (χωρητ)
ΓΡΑΨΕ 'Οι επιτηρητές για αυτήν την αίθουσα είναι ', επιτηρητές
σύνολο <– σύνολο + χωρητ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΤΕΛΟΣ_ΠΡΟΓΡΑΜΜΑΤΟΣ ΑΣΕΠ
! ==================================================
ΣΥΝΑΡΤΗΣΗ Πόσοι_επιτ(αριθμός): ΑΚΕΡΑΙΑ
ΜΕΤΑΒΛΗΤΕΣ
ΑΚΕΡΑΙΕΣ : αριθμός, πλ
ΑΡΧΗ
ΑΝ (αριθμός <= 15) ΤΟΤΕ
πλ <– 1
ΑΛΛΙΩΣ_ΑΝ (αριθμός <= 23) ΤΟΤΕ
πλ <– 2
ΑΛΛΙΩΣ
πλ <– 3
ΤΕΛΟΣ_ΑΝ
Πόσοι_επιτ <– πλ
ΤΕΛΟΣ_ΣΥΝΑΡΤΗΣΗΣ |
ΘΕΜΑ 4ο
Για την παρακολούθηση των θερμοκρασιών της επικράτειας κατά το μήνα Μάιο καταγράφεται κάθε μέρα η θερμοκρασία στις 12:00 το μεσημέρι για 20 πόλεις. Να σχεδιάσετε αλγόριθμο που:
α. θα διαβάζει τα ονόματα των 20 πόλεων και τις αντίστοιχες θερμοκρασίες για κάθε μία από τις ημέρες του μήνα και θα καταχωρεί τα στοιχεία σε πίνακες. Μονάδες 2
β. θα διαβάζει το όνομα μίας πόλης και θα εμφανίζει τη μέγιστη θερμοκρασία της στη διάρκεια του μήνα. Αν δεν υπάρχει η πόλη στον πίνακα, θα εμφανίζει κατάλληλα διαμορφωμένο μήνυμα. Μονάδες 9
γ. θα εμφανίζει το πλήθος των ημερών που η μέση θερμοκρασία των 20 πόλεων ξεπέρασε τους 20
οC, αλλά όχι τους 30 οC.
Μονάδες 9
| Λύση |
Αλγόριθμος ΕΜΥ
Για i από 1 μέχρι 20 ! ερώτημα α
Διάβασε ΠΟΛΗ[i]
Τέλος_επανάληψης
Για i από 1 μέχρι 20
Για j από 1 μέχρι 31
Διάβασε ΘΕΡΜ[i, j]
Τέλος_επανάληψης
Τέλος_επανάληψης
Διάβασε όνομα_πόλης ! σειριακή αναζήτηση
βρέθηκε ← ψευδής
pos ← 0
i ← 1
Όσο (βρέθηκε = ψευδής) και (i <= 20) επανάλαβε
Αν (ΠΟΛΗ[i] = όνομα_πόλης) τότε
βρέθηκε ← αληθής
pos ← i
Αλλιώς
i ← i + 1
Τέλος_αν
Τέλος_επανάληψης
Αν (βρέθηκε = αληθής) τότε
μέγιστος ← ΘΕΡΜ[pos, 1] ! εύρεση μεγίστου στη γραμμή pos
Για j από 2 μέχρι 31
Αν (ΘΕΡΜ[pos, j] > μέγιστος) τότε
μέγιστος ← ΘΕΡΜ[pos, j]
Τέλος_αν
Τέλος_επανάληψης
Εμφάνισε μέγιστος
Αλλιώς
Εμφάνισε "Δεν υπάρχει πόλη με αυτό το όνομα"
Τέλος_αν
πλήθος ← 0 ! ερώτημα γ
Για j από 1 μέχρι 31
άθροισμα ← 0
Για i από 1 μέχρι 20
άθροισμα ← άθροισμα + ΘΕΡΜ[i, j]
Τέλος_επανάληψης
!δεν είναι απαραίτητη η χρήση πίνακα, δεν χρειάζεται η τιμή στη συνέχεια
μο ← άθροισμα / 20 ! μέσος όρος της ημέρας j για όλες τις πόλεις
Αν μο > 20 και μο <= 30 τότε
πλήθος ← πλήθος + 1
Τέλος_αν
Τέλος_επανάληψης
Εμφάνισε "Το πλήθος είναι ", πλήθος
Τέλος ΕΜΥ |
Ημερομηνία τελευταίας τροποποίησης: 30/5/2006
Επικοινωνία: Τσιωτάκης Παναγιώτης